Top 20 FAQs on Moment of Inertia with Answers
1. What is the moment of inertia?
The moment of inertia is a measure of an object’s resistance to rotational motion about an axis. It depends on mass distribution and the rotation axis.
2. What is the formula for the moment of inertia?
The general formula is:
I=∑miri2I = \sum m_i r_i^2
For continuous objects, it’s expressed as:
I=∫r2dmI = \int r^2 dm
3. How is the moment of inertia different from mass?
Mass is a measure of inertia in linear motion, while the moment of inertia applies to rotational motion and depends on both mass and its distribution.
4. What are the SI units of the moment of inertia?
The SI unit of the moment of inertia is kg·m² (kilogram meter squared).
5. How does the moment of inertia affect rotational motion?
A higher moment of inertia means more resistance to rotational acceleration, requiring more torque to achieve the same angular acceleration.
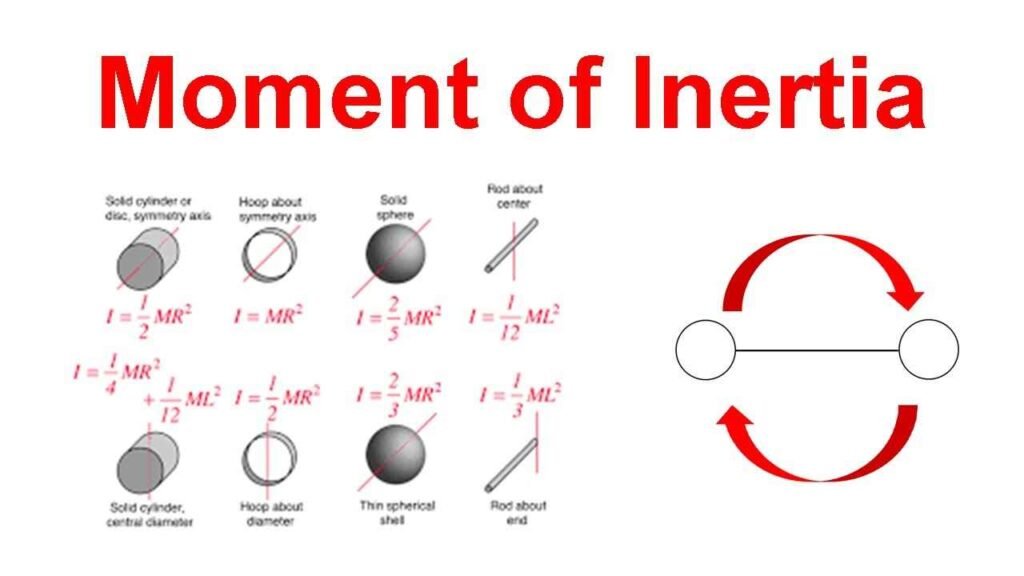
6. How is the moment of inertia calculated for different shapes?
Each shape has a unique formula based on mass distribution. Examples:
- Solid sphere: I=25MR2I = \frac{2}{5} MR^2
- Hollow sphere: I=23MR2I = \frac{2}{3} MR^2
- Solid cylinder: I=12MR2I = \frac{1}{2} MR^2
- Thin rod (center): I=112ML2I = \frac{1}{12} ML^2
7. What is the physical significance of the moment of inertia?
It determines how easily an object can rotate. A lower moment of inertia allows faster rotation for the same applied torque.
8. What is the parallel axis theorem?
It states that if you know the moment of inertia about the center of mass (IcmI_{cm}), you can find it for any parallel axis at distance dd:
I=Icm+Md2I = I_{cm} + Md^2
9. What is the perpendicular axis theorem?
For a 2D object, the moment of inertia about the z-axis is the sum of its moments of inertia about the x- and y-axes:
Iz=Ix+IyI_z = I_x + I_y
10. How does the moment of inertia affect angular momentum?
Angular momentum (LL) is given by:
L=IωL = I\omega
A higher moment of inertia results in greater angular momentum for a given angular velocity.
11. How does mass distribution affect the moment of inertia?
If more mass is farther from the axis, the moment of inertia increases, making it harder to rotate the object.
12. What happens to rotational motion if the moment of inertia changes?
According to conservation of angular momentum, if the moment of inertia decreases (e.g., a skater pulling arms in), angular velocity increases.
13. Why do figure skaters spin faster when they pull in their arms?
By pulling their arms inward, they decrease their moment of inertia, and due to conservation of angular momentum, their rotational speed increases.
14. Why is the moment of inertia important in engineering?
It’s crucial in designing flywheels, gears, rotating machinery, spacecraft, and even bridge stability under rotational forces.
15. How is the moment of inertia used in sports?
- In gymnastics and diving, body positioning controls spin.
- In cricket and baseball, bat weight distribution affects swing speed.
- In cycling, wheel mass affects acceleration and stability.
16. How does the moment of inertia affect vehicle dynamics?
A lower moment of inertia in cars allows quicker acceleration, while a higher moment of inertia in flywheels improves engine efficiency.
17. What is the role of the moment of inertia in robotics?
It helps in designing robotic arms and balancing mechanisms by optimizing rotational motion and control.
18. Can two objects with the same mass have different moments of inertia?
Yes, the moment of inertia depends on how mass is distributed relative to the rotation axis, not just the total mass.
19. How is the moment of inertia related to torque?
According to Newton’s second law for rotation:
τ=Iα\tau = I\alpha
where τ\tau is torque, II is the moment of inertia, and α\alpha is angular acceleration.
20. What is the moment of inertia of the Earth?
The Earth’s moment of inertia about its axis is approximately 8.04×10378.04 × 10^{37} kg·m², affecting its rotational motion and precession.